Tensile Testing Machines

Back to Index

Tensile Properties of Polymers

The tensile properties of polymers are important for the design of plastic parts and the prediction of their performance under stress, particulalry when used in structural applications. The simplest case are homogeneous isotropic materials. For these materials, the mechanical response depends on only two constants, the Young modulus E, and the Poisson ratio ν, whereas for anisotropic materials such as oriented-amorphous or oriented-crystalline polymers more constants are required to describe the mechanical response. Below, only isotropic materials will be considered.

At low strain (< 1 %), the deformation of most polymeric materials is elastic, that is, the deformation is homogenous and after removal of the deforming load the material returns to its original size and shape. In this regime, the stress (σ) is directly proportional to the strain (ε), meaning, the material obeys Hooke's law:

σ = E ε

where E is the Young's modulus (also called elastic modulus or tensile modulus. It is the slope of the stress-strain curve, i.e., the ratio between an incremental increase in applied stress, Δσ, and an incremental deformation, Δε. It is a measure for the stiffness of a material. The reciprocal of the Young's modulus is the tensile compliance, D, defined by

ε = D σ

In a static stress-strain experiment, a sample is pulled at a constant elongation rate and the stress, σ, is measured as function of strain, ε. A typical tensile test specimen is shown below.1

Tensile Test Specimen

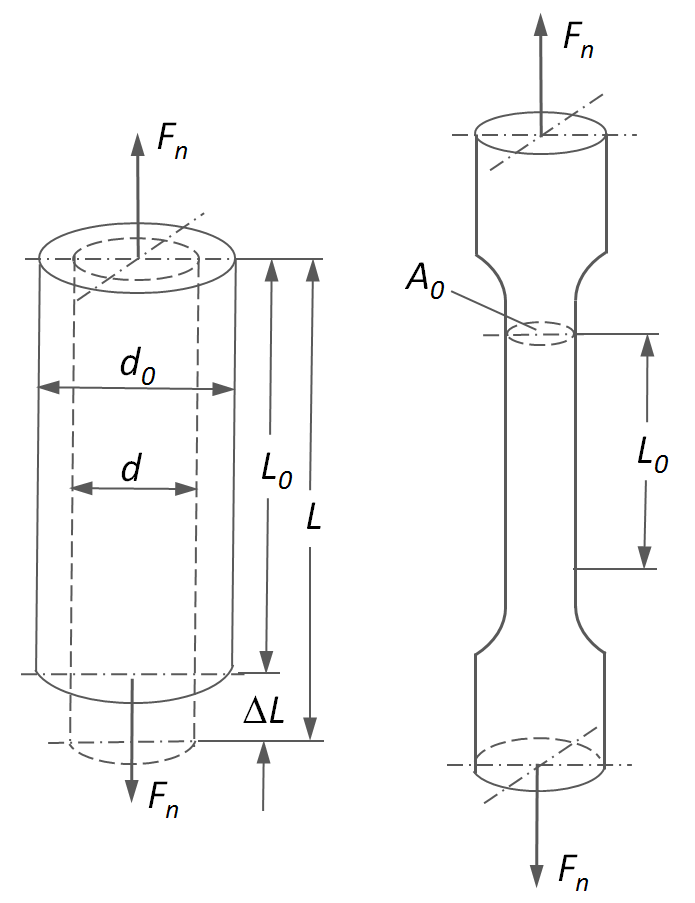
CROW logo

In most cases, the stress-strain response of a tensile sample is reported in terms of nominal or engineering stress and strain. The nominal or engineering tensile stress is defined as the force divided by the initial (undeformed) cross-sectional area:

σe = F / A0

and the engineering tensile strain or Cauchy strain is defined as the elongation, ΔL, divided by the initial (undeformed) length of the specimen, L0:

εe = ΔL / L0

Alternatively, the stress-strain response of a tensile sample may be reported in terms of true stress and true strain. The true stress is the ratio of the applied load to the actual cross-sectional area at a given elongation:

σt = F / A

If the volume of the test specimen is constant during deformation, it follows

L / L0 = A / A0

Thus

σt = F / A0 · (A0 / A) = σe · (L0 / L)

The true strain (also called Hencky strain2 or logarithmic strain) is the sum or integral of all incremental length changes, dL, divided by the actual length L:

εT = ∫ dL / L = ln(L / L0)

The relationship between true strain and engineering strain is simply

εT = ln(L / L0) = ln[(L0 + ΔL) / L0] = ln(1 + εe)

These relations are only valid up to the onset of necking. Beyond this point, strong necking will result in a change in volume.

For small elongations, true stress and engineering stress are essentially the same, whereas for large elongations the true strain and stress are preferred.

References and Notes
  1. Round tensile dog-bones are a common geometry for metal tensile testing whereas flat dog bones are more commen for plastics.
  2. H. Hencky, Zeitschrift fuer Technische Physik, 9, 215 (1928)

  • Summary

    Tensile Strength

    In a static tensile stress-strain test, the stress is measured as a function of elongation at a constant deformation rate. Usually, the engineering (nominal) stress is plotted as a function engineering strain.

  • The engineering strain is the elongation divided by the inital length and the engineering stress is the axial load divided by the initial cross-sectional area perpendicular to the force.

  • Alternatively, the stress-strain response of a tensile sample may be reported in terms of true stress and true strain. For small elongations (< 0.1%), true stress and engineering stress are essentially the same.

  • At low strain, the deformation of most polymeric materials is elastic and the measured stress is directly proportional to the strain (Hooke's law).

  • The ratio of stress and strain is called the tensile modulus of elasticity E which is also known as the Young's Modulus. It is a measure for the stiffness of a polymer.

  •